Gaussian 09 Revision D.01 is now available in the HPC systems. With the current LSF job scheduler configuration and the hardware resources available, you may be wondering how you can run large Gaussian jobs more efficiently and get results faster. This article explores ways to do so through a few case studies.

Some shared memory parallel jobs for geometry optimization run using Density Functional Theory method B3LYP and 6-31+g(d,p) basis set. All jobs are submitted to “large” queue with different number of processors specified in the input file (nprocshared=n). Same memory size (2GB) is specified for each job. The jobs are executed on the atlas7 cluster fat nodes (Node specifications: Xeon CPU E7- 4860 @2.27GHz and 264GB RAM).  As the atlas7 cluster fat nodes have 4 10-core processors on each nodes, all jobs run within one node in a shared memory mode. The following table and figure show the turnaround time of each job versus the number of processors used.

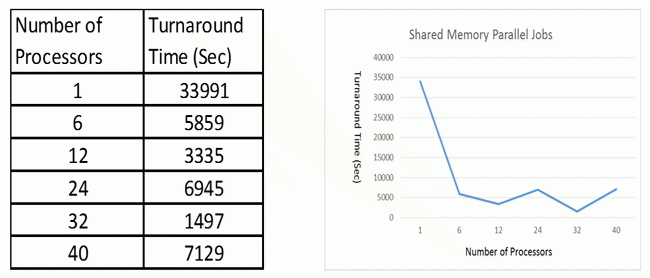
Although more processors can help reduce the turnaround time of a job, the results are inconsistent. We note that jobs do not scale very well when the processor number exceeds 12. One possible reason could be that the jobs are not executed on dedicated resources and there are other users’ jobs running on the same node competing with the Gaussian jobs for CPU resources.  However, good performance can still be achieved with more processors in some cases.  In this case study, when the number of processors is set to 32, the turnaround time of the job is only 1/23 of that for the serial job in which the number of processor is set to 1.

Gaussian uses Linda parallel to run parallel jobs across multiple nodes. The Linda parallel jobs were submitted to “parallel” queue using g09linda executable. The jobs run in shared memory parallel mode within one node (nprocshared=12) and Linda parallel mode among multiple nodes. These jobs are executed on atlas6 compute nodes (Node specifications: Xeon CPU X5650 @2.67GHz, 49GB RAM).

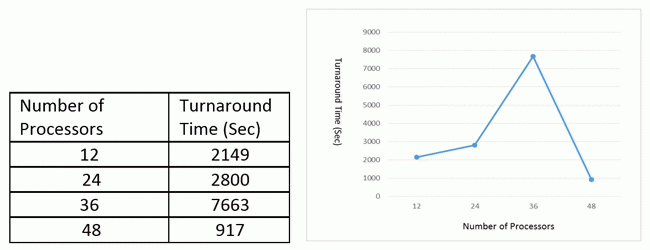
The results given above show that when Linda parallel jobs run on only one node with 12 processors, the performance has a linear scalability compared with serial jobs running with 1 processors. When Linda parallel jobs run with 24 and 36 processors, the performance become worse. However, we got an almost linear scalability when linda parallel jobs run with 48 processors. We are still investigating the reason behind this, but the recommendation is to run linda parallel jobs using 12 processors for small jobs, and 48 processors for large Gaussian jobs.

Gaussian SCF energy and gradient calculations (geometry optimizations) have very modest memory requirements. The memory specified with “%mem” in the input files is shared by all processors in “%nprocshared”. For SCF energy and gradient calculations it is recommended to use a minimum of 256 MB of memory per processor, which means “%mem=3GB” if using “%nprocshared=12”.

The following table and graph show how different memory affect the turnaround time of the Gaussian geometry optimization jobs. All jobs were submitted to the parallel queue using 12 processors with parallel linda executables.

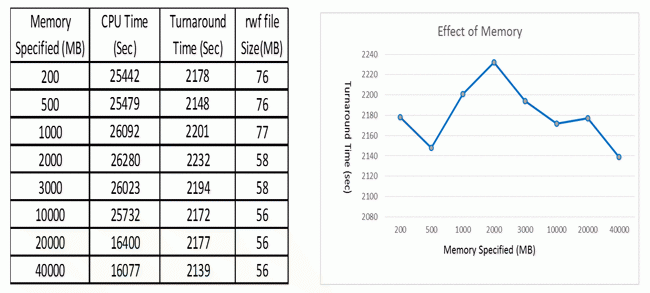
Results shows that having more memory does not help the job performance in this case. The differences between the turnaround time for all the jobs are within 4%. As mentioned earlier, energy and gradient calculations have very modest memory requirements, an increase in memory will not  bring much change to the job performance.  A change would happen only when the amount of memory is large enough that the SCF procedure switches to the “in-core” algorithm instead of the default “direct” algorithm. The “in-core” algorithm can be faster than the “direct” algorithm when running on one processor. However, for a small job like this one, the “in-core” algorithm is not going to scale well with an increasing number of processors as the “direct” algorithm. One can suppress the use of the SCF “in-core” algorithm with the “SCF=NoInCore” keyword.

Based on the above benchmark results, the follows are some recommendation for running Gaussian jobs more efficiently:

1. Submit small Gaussian jobs to serial queues with different number of processors specified: https://comcen.nus.edu.sg/services/hpc/application-software/gaussian. Multiple jobs can be submitted to different queues so you can have as many jobs to run as the system configuration permits.
2. Larger Gaussian jobs can be submitted to “parallel8” and “parallel” using Linda parallel executable. But set “-np” to 8 or 12 only. This will ensure your jobs be dispatched earlier and run on dedicated node, thus have better performance.
3. Long running jobs can be submitted to “parallel” queue using Linda parallel executable with 48 processors, which is the largest number of processors allowed in the parallel queue.

Specify a minimum of 2GB and 3GB memory for jobs submitted to “parallel8” and “parallel”. More memory will not have much effect for energy and gradient calculations unless you use “SCF=NoInCore” key word in your input files.