NORMAL MODE ANALYSIS OF NANO-STRUCTURE USING TIME DOMAIN DECOMPOSITION OPERATIONAL MODAL ANALYSIS
Introduction
In this report, we present an operational modal analysis technique to determine the vibration frequencies and mode shapes of nano-structures. There are two approaches for calculating the vibration frequencies and mode shapes of nano-structures. The first approach is eigenvalue frequency analysis. In this method, the Hessian matrix for a given atomic configuration needs to be constructed. Next, the dynamic matrix is constructed by scaling the Hessian matrix with the atomic masses. Eigenvalue analysis of the dynamic matrix is performed to obtain the frequencies and mode shapes. The Hessian matrix is constructed by taking the second gradient of the interatomic potential energy function with respect to atomic positions. For a simple interatomic potential, the Hessian matrix can be derived analytically. However, for complicated interatomic potentials, the finite difference scheme is usually adopted to obtain the Hessian matrix. It is very computationally intensive to construct the Hessian matrix for large atomic systems and for complicated inter-atomic potentials such as AIREBO potential (Stuart et al. 2000). The second approach is the normal mode analysis that is commonly used in structural health monitoring where the structure vibration frequencies and mode shapes are extracted from ambient vibration data. Time domain decomposition operational modal analysis (TDDOMA) technique belongs to the latter category (Odeja 2000). TDDOMA was developed to estimate vibration frequencies and mode shapes of buildings and bridges. For the first time we employ the TDDOMA technique to calculate the vibration frequencies and mode shapes of nanostructures.
Implementation of TDDOMA Technique
The TDDOMA technique consists of four stages: (i) obtain atomic trajectories using atomistic simulations, (ii) calculate auto-correlation function and obtain the Fourier spectrum, (iii) calculate the modal frequencies by peak picking method, (iv) filter the time history around the modal frequency and perform singular value decomposition to get the mode shapes. For TDDOMA analysis, the atomistic trajectories were extracted from classical molecular dynamics (MD) simulation. MD simulations were performed using LAMMPS (Plimpton 1995) in the NUS-HPC cluster. The TDDOMA method was implemented in a FORTAN90 code. This code reads the atomic displacement time histories from MD simulations and performs Fourier transform using FFT routines available in the DFFTPACK library. Auto-correlation spectrum was obtained and the vibration frequencies were determined using the peak picking method. The Butterworth band-pass filter was used to extract the time histories at the desired modal frequencies. The auto-correlation matrix was calculated from the filtered time histories. The multiplication routine DGEMM available in DFFTPACK library was used to carry out all the matrix multiplications required to construct the response matrix. After that, singular value decomposition was performed on the response matrix using DGESVD subroutine to get the mode shapes. The proposed method can be applied to any nano-structure. For demonstration purpose, the case studies are presented next.
Results and Discussions
In this section, three case studies are cited. The case studies were performed on single-walled carbon nanotube (SWCNT) that has a cylindrical shell-like structure with the shell walls made of one-atomic layer thick carbon atoms and g-graphyne that is a 2-D nano-sheet made of carbon atoms. The first two case studies were performed on short and long single walled carbon nanotubes clamped at either ends. For the third case study g-graphyne which is a 2-D nano-sheet clamped at the four edges was chosen.
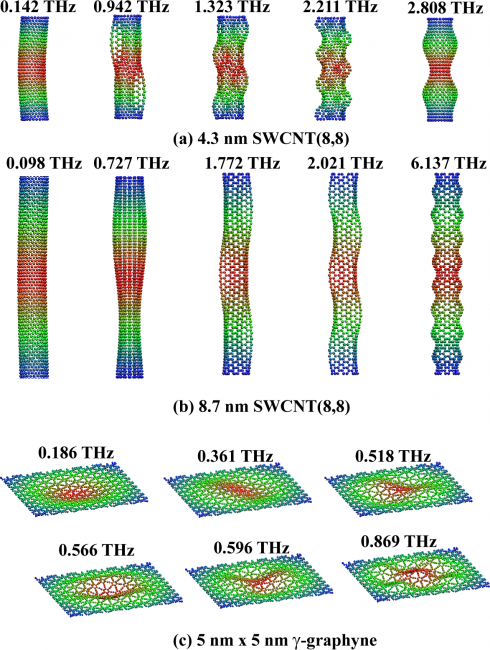
Acknowledgement
We express our earnest thanks to NUS Computer Centre for providing us with the excellent computational facilities. We thank the NUS HPC personnel for their beneficial and prompt responses.
References
Stuart, S. J., Tutein, A. B., and Harrison, J. A. (2000). “A reactive potential for hydrocarbons with intermolecular interactions.” J Chem Phys 112, pp. 6472-6486.
Odeja, A. P. (2012). “Matlab implementation of an operational modal analysis technique for vibration-based structural health monitoring ” Masters of Engineering, Massachusetts Institute of Technology.
Plimpton, S. (1995). “Fast parallel algorithms for short-range molecular dynamics.” Journal of Computational Physics 117, pp. 1-19.

