DIRECT NUMERICAL SIMULATION OF OSCILLATORY FLOW OVER RIPPLED-BED USING FOURIER-SPECTRAL/HP ELEMENT DISCRETIZATION
Introduction
While propagating on shallow waters, moderate sea waves produce wavy patterns or ripples in sand. Despite the simple form of these ripples, the oscillatory flow around them is highly complex. Turbulent vortices are created at each period, and these structures suspend high amounts of sediment until they eventually decay, and deposit the sediments onto troughs of the ripples. A good understanding of this intricate flow-physics is essential for accurate prediction of the involved sediment transport.
With the increasing availability of high-performance computing (HPC) platforms, direct numerical simulation (DNS) of turbulent flows are establishing themselves as a strong alternative to laboratory experiments. In DNS, all the scales of turbulent motion are resolved, and the flow is simulated with maximum realism. In a typical DNS experiment, an extensive database with three-dimensional snapshots of the flow is created. This database contains information about the key flow properties such as form drag, skin friction, vortex-circulation and dynamics, which are difficult to measure accurately even in the state-of-the art laboratory experiments. Therefore, despite its great cost, DNS is a valuable complement to field and laboratory measurements.
In this work, we perform DNS of an oscillatory flow over a rippled-bed using the open-source spectral/hp element framework Nektar++[1]. The primary objective is to elucidate the mechanisms in vortex creation, interaction and decay, and the associated induced-drag and skin-friction. Special attention is paid to flow configuration to be similar to full-scale field conditions, which correspond to high Reynolds numbers (Re~10000). Resolving all the scales of a turbulent motion requires a grid resolution scaling with approximately Re^(9/4). Therefore, the study requires a state-of-the art HPC platform such as the new petascale supercomputer of National Supercomputer Center (NSCC) of Singapore.
Methodology
DNS requires high-order numerical methods to avoid numerical diffusion altering the physics of the flow. Traditionally, DNS is conducted for theoretical flows with simple geometries like isotropic turbulence in periodic boxes or canonical shear flows. In these studies, Fourier-pseudospectral methods have been the main workhorse due to its simplicity and high-convergence rates. However, this method requires periodic domains, and therefore, can only be employed in homogeneous directions.
In this respect, hp-FEM discretization in Nektar++ provides a geometrically flexible method with high-order accuracy. Moreover, Nektar++ also allows the combination of hp-Fem with Fourier-pseudospectral discretization, if the flow contains homogeneity. This strategy is very suitable for the flow over two-dimensional ripple shapes, where the problem exhibits translation symmetry in the spanwise direction, hence homogeneity.
In this study, we employ a mixed representation, where an unstructured grid with two-dimensional quadrilateral elements is utilized in streamwise-wall normal (x-y) plane, and Fourier expansions are considered in the homogeneous (z) direction [2,3]. The quadrilateral elements are equipped with tensor-product of one-dimensional hierarchical expansion basis with an order of p=6. The spatial discretization is achieved using a continuous Galerkin approach. The resulting system of differential algebraic equations is discretized in time using a second-order implicit scheme. Finally, the coupled linear system of equations are segregated using a velocity-correction scheme, and individual parts are solved with an iterative solver based on static condensation.
The computational domain is designed by taking into account the effects of periodicity in spanwise and streamwise directions, and the motion of the ejected vortex from ripples. The domain contains three ripples, i.e., Lx /λ = 3, has a significant spanwise length of Lz /λ = 6 to prevent periodicity effecting instability of the main vortex, and has a vertical extend of Ly/λ=1.5λ. Ripples have a smooth wall with prescribed no-slip velocity, and a symmetry boundary condition is applied on the top boundary. The flow is driven with a simple harmonic pressure gradient, which induces a sinusoidal free-stream velocity.
The simulation is run on the petascale supercomputer of National Supercomputer Center (NSCC) of Singapore using 2160 cores of Intel Xeon dual socket E5-2690v3 CPUs, and message passing interface (MPI) parallelization. We resolve each period of the flow with 80000 time steps. Maximum CFL number remains around 0.4 for this resolution. The simulation ran through 10 periods of initial transient. The data is being collected currently for statistical analysis using 64 snapshots each period.
Results
In this section, we present the preliminary results. Figure 1 shows an instantaneous snapshot of the flow using a positive isosurface of Q-criterion, a vortex-identification method marking the regions where vorticity dominates over strain, at phase theta=pi/8. The spanwise vortex, which is created during the separation, ejects itself with its self-induced velocity. The structure is highly turbulent with circular-like vortex elements wrapped around it. Close to the wall, there are stream wise structures in the form of counter-rotating vortices, which are produced by extensional strain fields and concentration of vorticity.
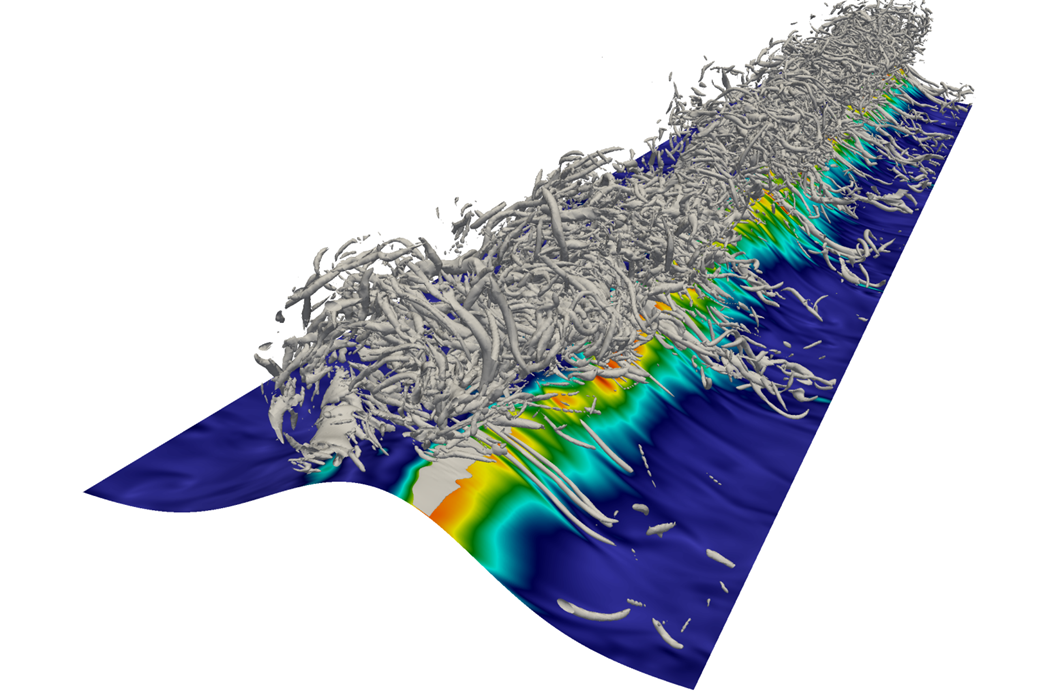
Vortex formation and ejection cycle and the corresponding shear-stress distribution on the ripple are shown in Figure 2. The motion of the main vortex can be tracked with the Reynolds-averaged span wise vorticity. We see that during the flow reversal (Fig. 2a) a strong separation region with a positive sense of circulation (red) exists. Moreover, a weak free-vortex with negative circulation (blue) from previous cycle approaches the ripple. The separated flow further evolves into a large circular vortex (red) while the weak vortex becomes diffused (Figure 2b-d). In Figure 2e, the free-stream velocity diminishes, and the main vortex induces separation on the wall with opposite sense of rotation (blue). The main vortex (red) and the separated vortex (blue) start to eject themselves with their self-induced velocity (Figure 2f). Note that in this process the negative-vorticity (blue) is transferred to the other side of the ripple. This implies that the introduction of the negative circulation to the other side of the ripple takes place while free-stream velocity is still weak. Later on in Figure 2g, the ejection continues, and two vortices with opposite sense of rotation eventually decouples (Figure 2h).
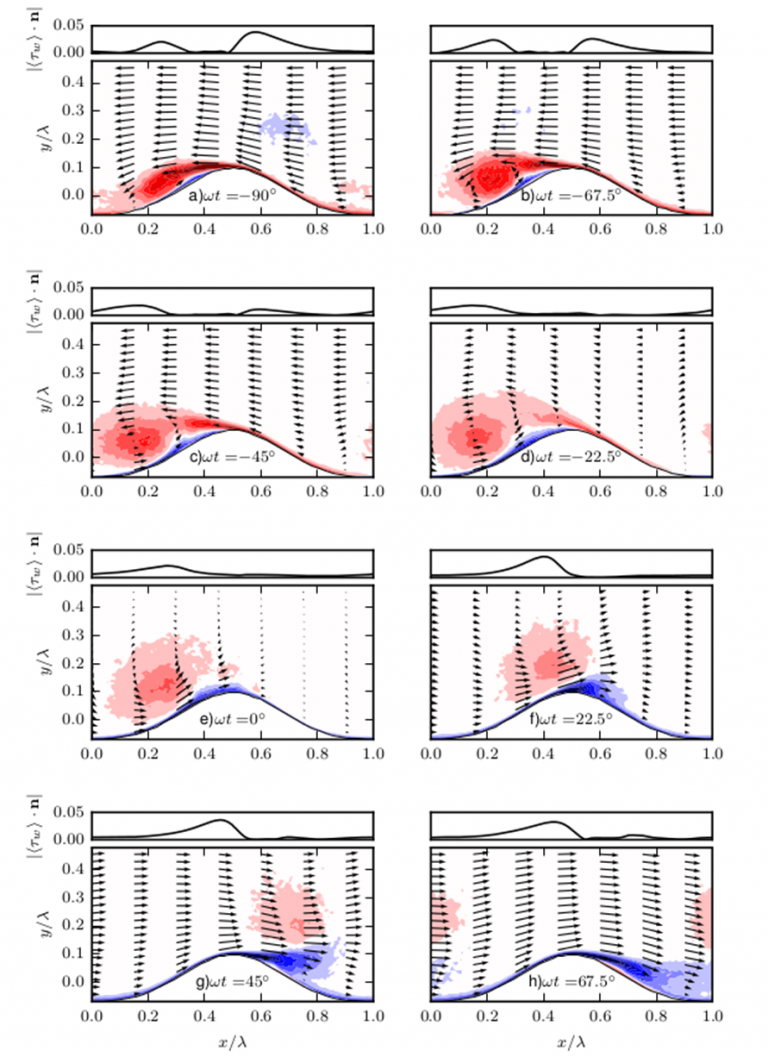
We are currently investigating the form drag and skin-friction over the cycle and their relation to vortices. We will also study turbulent kinetic energy, and enstrophy budgets when more flow data is available.
Acknowledgements
This research is under the Tier-1 project “Sheet-flow sediment transport in the coastal environment” funded by the Ministry of Education. I would like to acknowledge the support of Dr. Wang Junhong, Paul Hiew and NSCC-helpdesk team (esp. Srikanth Gumma).
References
- Cantwell, Chris D, Moxey, David, Comerford, A, Bolis, A, Rocco, G, Mengaldo, G, De Grazia, D, Yakovlev, Sergey, Lombard, J-E, Ekelschot, D & others (2015), Nektar++: An open-source spectral/hp element framework. Computer Physics Communications 192, 205–219.
- Karniadakis, GE (1990), Spectral element-Fourier methods for incompressible turbulent flows. Computer Methods in Applied Mechanics and Engineering 80 (1), 367–380.
- Karniadakis, GE & Sherwin, SJ (2005), Spectral/hp methods for computational fluid dynamics.

