THE BENCHMARK TEST OF A PARALLEL SPATIAL AGENT-BASED MODEL USING 128 CORES
Introduction (The Schelling model)
The utilization of HPC for spatial simulation has been an uncharted territory for most social scientists. However, it is crucial for social scientists to take advantage of the power of HPC so that complex geospatial phenomena can be simulated and thereby understood. This research aims to present the benefits of parallel computing for understanding geospatial phenomena. With the motivation, the Schelling model was parallelized. The Schelling model has been used to simulate residential segregation by ethnic groups for decades. In the Schelling model, agents–households and housing units–determine movements by satisfaction with their neighborhoods (Schelling 1971). The satisfaction is calculated based on the proportion of households of their own group and other groups. However, since the Schelling model has been implemented with artificial worlds, there are limitations to describe the phenomena of the real world. One of the reasons is the computing intensity of the model. The parallelization of the model can address the issue, and allow us to build a more accurate model of the complex real-world phenomena. This article shows how data decomposition methods influence the performance of a spatial agent-based model.
The parallelization of the Schelling model
The study area was the County of San Diego in the U.S. Households and housing units were created based on the 2000 U.S. Decennial Census. Since agents can move over the spatial data domain, i.e., the spatial extent of San Diego County, the decomposition of the data domain is challenging for the parallelization of the Schelling model. Nine different domain decomposition methods (Figure 1) were experimented with the benchmark test. The equal area decomposition methods partition the spatial domain into subdomains of the same areas, while the unequal area and the irregular shape decomposition methods partition the spatial domain into subdomains of approximately the same number of agents. The decomposition can also be carried out in different directions, including column-wise, row-wise, and block-wise. Together nine decompositions shown in Figure 1 were tested. The parallel Schelling model was iterated 120 times for the 10 year simulation. The benchmark test was performed on the atlas5 cluster.

Performance Results and Discussion
Figure 2 shows the speed up and efficiency of the benchmark test. As the number of CPU cores increases, the computing time decreases. The equal area decomposition methods show poor performance, but unequal area decomposition methods and irregular shape decomposition methods show better performance. For the directional decomposition methods, row-wise methods show the best performance.
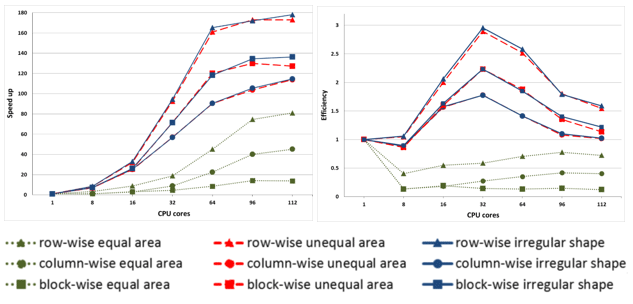

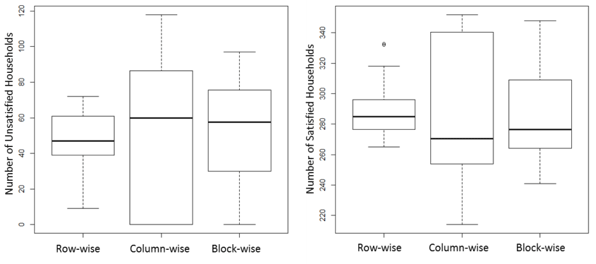
In San Diego County, most people live in coastal areas. We assume that the performance differences are due to the spatial distribution of agents representing these people. For equal area decomposition methods, some subdomains can have more agents than other subdomains because of the irregular spatial distribution of agents. Additionally, if the spatial domain is decomposed by the column-wise methods, it is highly likely that some subdomains including the coastal areas can have more agents and lead to the poor performance of overall parallel processing. Figure 4 shows box plots illustrating the irregular distribution of agents in subdomains.
Conclusion
This article presents the close relationship between the spatial data decomposition methods and the performance of a spatially explicit agent-based model. The spatial heterogeneous distribution of agents influences the performance of the parallel application. The performance results indicate that the spatial data should be decomposed with consideration of the irregular and dynamic spatial distribution of geospatial features.
Acknowledgement
We thank NUS Computer Center, specially Dr. Wang Junhong who allowed us to utilize 128 cores on atlas 5 for the benchmark test.
Reference
KIM, I.-H., TSOU, M.-H. and FENG, C.-C. 2015. Design and implementation strategy of a parallel agent-based Schelling model. Computers, Environment and Urban Systems, 49, 30-41.
SCHELLING, T. C. 1971. Dynamic models of segregation. Journal of Mathematical Sociology, 1, 143-186.

