FREE ENERGY LANDSCAPE EXPLORATION USING GROMACS
Introduction
Free energy is the thermodynamic quantity of potential importance, because it reflects the intrinsic characteristics of targeting systems. In a closed system, free energy always gets minimized, while the overall randomness increases (i.e., maximizing entropy, S). It guides the evolution of systems (biomolecules, in our case), and directly links to many behavior of interest, such as reaction rates, folding path or mechanical responses. Thus, one of the central tasks of molecular simulations is to thermodynamically explore the free energy landscape. Umbrella sampling is a useful statistical technique for obtaining such free energy profiles of biomolecules. Here, we illustrate the processes to achieve Helmholtz free energy profiles (Δ) through conducting DNA umbrella sampling molecular dynamics under NTV ensemble, as an example.
DNA molecular dynamics
MD Simulations
The MD simulations were prepared and ran using the latest GROMACS version 4.5.5 under the newest Parm99 force field with ParmBSC0 corrections. Before starting any simulation, a basic simulating unit (i.e., unit cell) was carefully constructed. (1) An initial atomic straight DNA structure with 20 bp was generated using X3DNA. (2) It was centered within a minimal rhombic dodecahedron unit cell, whose inscribed sphere diameter equals to the largest DNA extension plus an additional 3.2 nm for buffering purpose. (3) This unit cell was further prepared by filling the empty space with explicit TIP3P water, neutralizing the negative charges on DNA using sodium counter-ions, and replacing some water molecules by sodium chloride to achieve 150 mM ionic strength. (4) It was finalized by energy minimization using the steepest descent method to remove any energy unfavourable close contacts.
Based on such prepared unit cell, molecular trajectories were self evolved according to Newton’s law of motion, given a set of initial velocities randomly sampled from Maxwell-Boltzmann distribution. The unit cell was brought to correct ensemble, through thermolization using 200 ps velocity rescaling and 200 ps Parrinello-Rahman pressure coupling simulations to adjust its temperature and volume. Then, a 50 ns MD simulation, which includes 30 ns equilibration stage and 20 ns production stage, was executed using periodic boundary conditions, under NVT ensemble, with constant temperature of 300 K and volume up to ∼1170 nm3. This currently takes about 5 ns/day in NUS HPC with 12 core parallelization.
Conformational fluctuations and ΔA
In our system, the probability of DNA configurations in particular state is proportional to the Helmholtz free energy of that state, according to Boltzmann distribution. Here, we distinguish the conformations of DNA through its end-to-end distances (i.e., reaction coordinates). As a result, the probability density function about end-to-end distance, d, is expressed as,
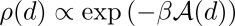
(1) where β rescales free energy into units of kBT. Thus, the free energy difference against reference state (i.e., DNA most possible free length, d0) can be easily evaluated from the ratio of occurrences of d against d0 in simulated trajectories,
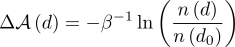
(2) However, as one may notice, the occurrences decrease very rapidly as d deviates from d0. Hence, for a typical “free” simulation (especially for a nanosecond timescale MD simulation), the distribution of d always equilibrates at d0 with a small variance; this information is usually insufficient to achieve the previously mentioned molecular behaviors. Special techniques, such as importance sampling, are necessary to broaden and accelerate the explorations of free energy landscape.
Umbrella sampling
Umbrella sampling is a type of importance sampling, which constraints conformational
; COM PULLING pull = umbrella pull_geometry = distance ; biased distance pull_k1 = 150 ; spring constant
fluctuations apart from “free” fluctuations, and exponentially boosts the occurrences of particular d using well-defined biased potentials. Usually, a series of such biased simulations are needed to evaluate Δ(d) at d far away from d0. Intuitively, the relative ratio of appearances can be worked out from nk (d) in kth simulation and n1 (d0) in 1th simulation (e.g., “free” simulation) , assuming that their relative weights are known,
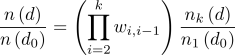
(3) ,where wi,i-1 is the occurrence weights of ith simulation against (i-1)th simulation. Thus, we have a way to expand and speed up the free energy landscape exploration.
In GROMACS, umbrella sampling is implemented by incorporating the above section of pulling codes into .mdp file before grompp. This implies a biased potential of i = κu (d – di)2 with spring constant κu and biased distance di to the system. After execution of simulations, the relative weights wi,i-1 are approximated through Weighted Histogram Analysis Method using g_wham. The figure below shows Δ(d) for our 20 bp DNA obtained by near equilibration simulation (red) and umbrella sampling (black), where interested DNA responses reside on small end-to-end distances, and are only accessible through biased simulations.
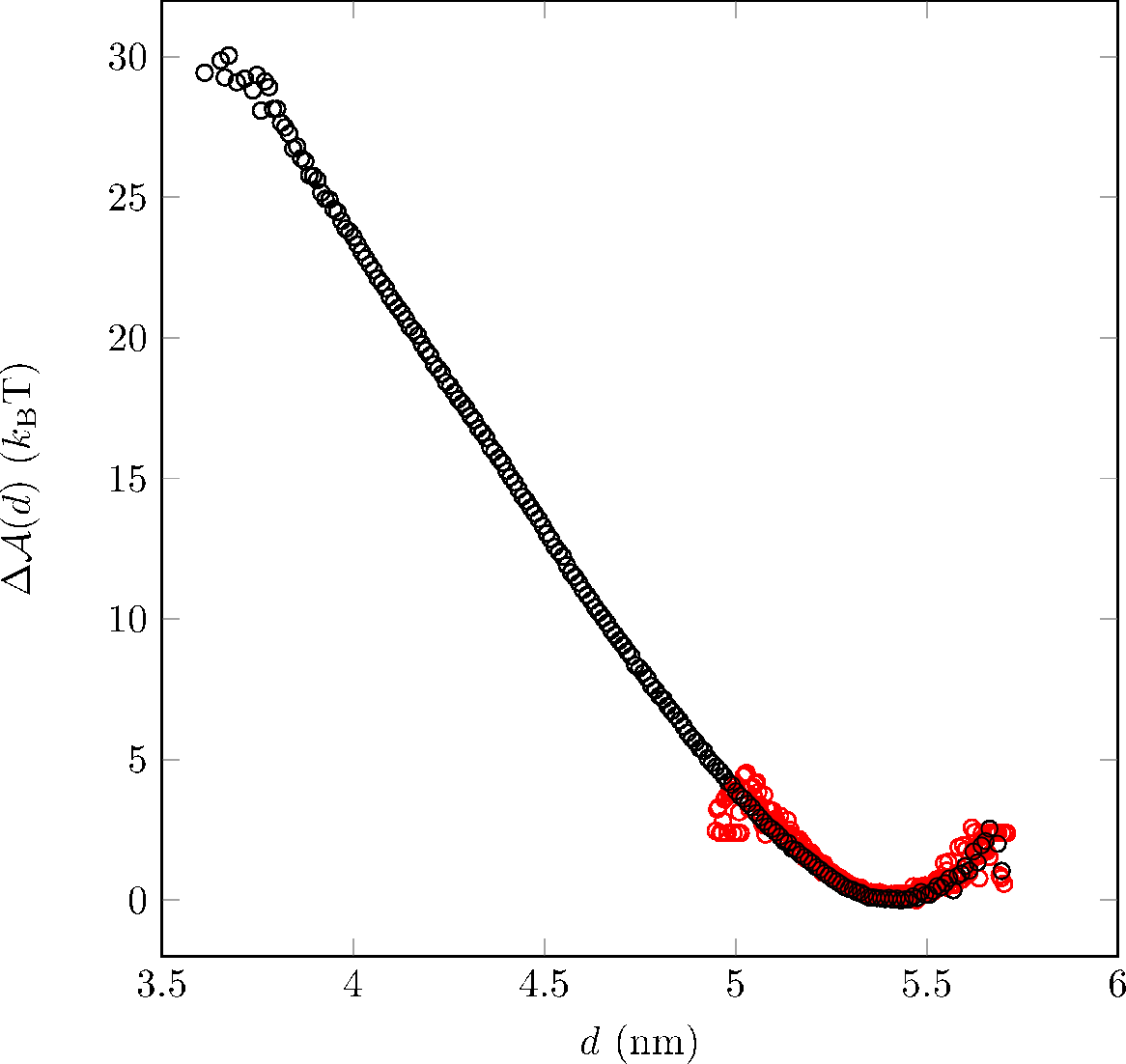
Figure 1: Free energy difference profile for DNA. Discretized Δ(d), reference to d0, separately obtained for near equilibration simulation (red) and umbrella sampling (black) are plotted against end-to-end distances. The two profiles overlap with each other near energy minimal state d0 ≈ 5.43 nm, while umbrella sampling explores a much wider free energy landscape.

